📖 [백준알고리즘 풀이] Q.1010 다리 놓기 문제 풀이 - java

📖 문제

https://www.acmicpc.net/problem/1010

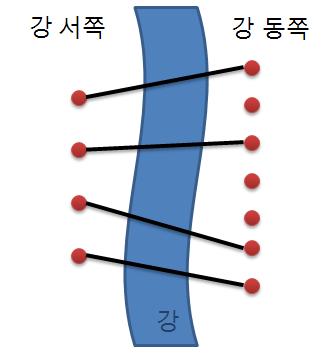
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다.

하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다.

강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의

서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)

재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.)

재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때

다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

example

🔍 접근법

Q.1010 다리 놓기 문제 풀이입니다.

문제에서 주어진 조건 중 가장 중요한 점은

다리가 엇갈리게 곂치지않아야 한다는 것입니다!

다리가 엇갈리지 안게 다리를 만드려면 경우의 수는 n<=m 일때만 성립하고

모두 1:1 대응이 되어아햡니다.

결과적으로 순서에 상관없이 m개 중 n개를 뽑는 경우의 수 (조합)이 답이 됩니다.

mCn = m-1 C r-1 + m C r-1 과 같습니다.

조합 전체 경우의수  = 어떤 한 원소를 이미 선택한 경우 + 하나의 원소를 선택하지 않을 경우의 수

이를 이용해 재귀적으로

public static int combination(int n, int r) {
        if (n == r || r == 0)
            return 1;
        else if(dp[n][r] > 0)
            return dp[n][r];
        else
            return dp[n][r] = combination(n - 1, r - 1) + combination(n - 1, r);
}

combination 함수를 통해 답을 구할 수 있습니다.

단 시간 소요를 줄이기 위해

동적프로그래밍의 메모이제이션을 통해 풀이합니다.

💻 코드

package problem.dynamic;

import java.io.*;

public class Main_1010 {

    static int n,m;
    static int T;
    static StringBuilder sb;
    static int dp[][];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        T = Integer.parseInt(br.readLine());
        sb = new StringBuilder();
        for(int i=0; i<T; i++){
            String[] temp = br.readLine().split(" ");
            n = Integer.parseInt(temp[0]);
            m = Integer.parseInt(temp[1]);
            dp = new int[m+1][n+1];
            sb.append(combination(m,n)+"\n");
        }
        bw.write(sb.toString());
        br.close();
        bw.flush();
        bw.close();
    }

    public static int combination(int n, int r) {
        if (n == r || r == 0)
            return 1;
        else if(dp[n][r] > 0)
            return dp[n][r];
        else
            return dp[n][r] = combination(n - 1, r - 1) + combination(n - 1, r);
    }
}

Written on February 9, 2021